Camera Calibration

An implementation of Tsai's camera calibration algorithm.

Introduction

Camera calibration is the process of estimating the parameters of a camera model order to create a model that approximates a physical camera. The resulting model describes the relationship between pixels in the image and rays of light in the real world.

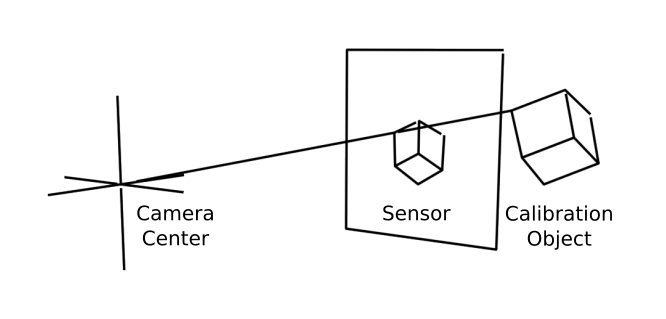Diagram of a simplified pinhole camera model The simplified pinhole camera model.

In this implementation a modified pinhole camera model with corrections applied to account for radial lens distortion is used to model the physical camera. Parameters such as focal length and position of the camera are recovered.

The photograph used as input needs to contain points with known geometry. For each of the points the coordinates in the real world (in millimeters) and the corresponding coordinates in the photograph (in pixels) are used as input to the calibration algorithm.

To estimate the parameters, a two-stage optimisation process is used. First, the parameters of a simplified linear model are estimated using a linear optimisation process (Singular Value Decomposition). In the second stage, the model is extended to include non-linear distortions, with a non-linear optimisation process (gradient descent) used provide the final estimates.

Example

In this example a photograph of a calibration object (two checkerboards attached at a right angle) was used to find the coordinates (in pixels) of several points on the obejct. These coordinates, along with their corresponding coordinates in millimeters are used as input to the algorithm.

Pictures

In the image below the red "actual" points are the input to the algorithm. The resulting model is then used to re-project the points onto the image using only the real-world (millimeter) coordinates - this is shown as the "projected" points. Adding non-linear distortion to the "projected" points results in the "distorted" points.

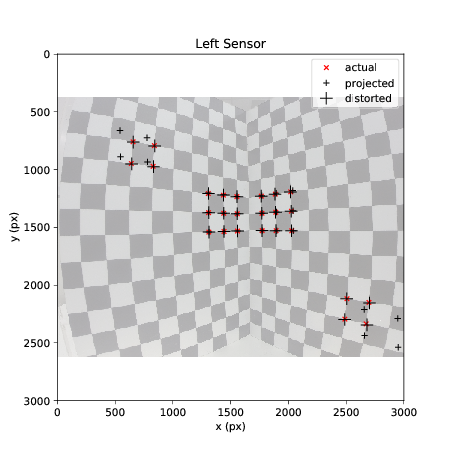
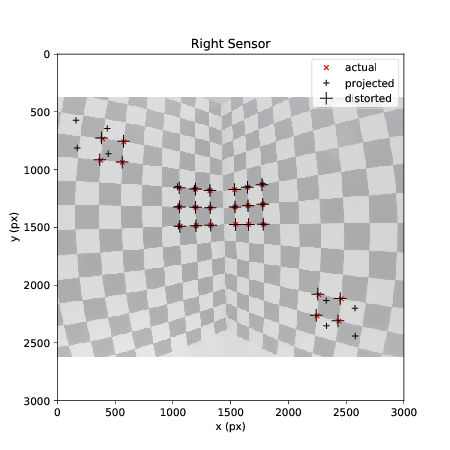
If the model is accurate the re-projected and distorted points should appear close to their "actual" locations.

Numbers

With a stereo pair (2 cameras), it's easy to measure the baseline (distance between the center of the cameras). Since the resulting model gives the positions of the cameras relative to the model, this can be calculated to the measurement. If you like looking at numbers I've included some in the table below.

	Measured	Calibration Result
		Left	Right	Stereo
Focal Length (mm)	3 (approx.)	1.89	1.93
First-order radial distortion (mm^-2)		-0.244	-0.240
Baseline (mm)	33			32.50
Camera-cube distance (mm)	233 (approx.)			251.0

Source

The source code is available from github.com/bailus/tsai-calibration

Requires

Python 2.x
- NumPy (Math library)
- Matplotlib (2D/3D plotting library)

References

R. Tsai, "A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses," in IEEE Journal on Robotics and Automation, vol. 3, no. 4, pp. 323-344, August 1987. web: ieee.org sci-hub.io doi: 10.1109/JRA.1987.1087109
Z. Zhang, "A Flexible New Technique for Camera Calibration," in IEEE Transactionson Pattern Analysis and Machine Intelligence, Vol. 22, No. 11, pp. 1330-1334, 2000. web: microsoft.com sci-hub.io doi: 10.1109/34.888718
W. Li, T. Gee, H. Friedrich, and P. Delmas, “A practical comparison between Zhang’s and Tsai’s calibration approaches,” in Proceedings of the 29th International Conference on Image and Vision Computing New Zealand, ser. IVCNZ ’14, Hamilton, New Zealand: ACM, pp. 166–171, 2014. ISBN: 978-1-4503-3184-5. web: acm.org sci-hub.io doi: 10.1145/2683405.2683443